Deel 3 - opgaveset 1#
In deze opgave gaan we op basis van de test-data bepalen hoe goed ons eerder getrainde netwerk is. Download hiervoor de opgaven vanuit deze zip.
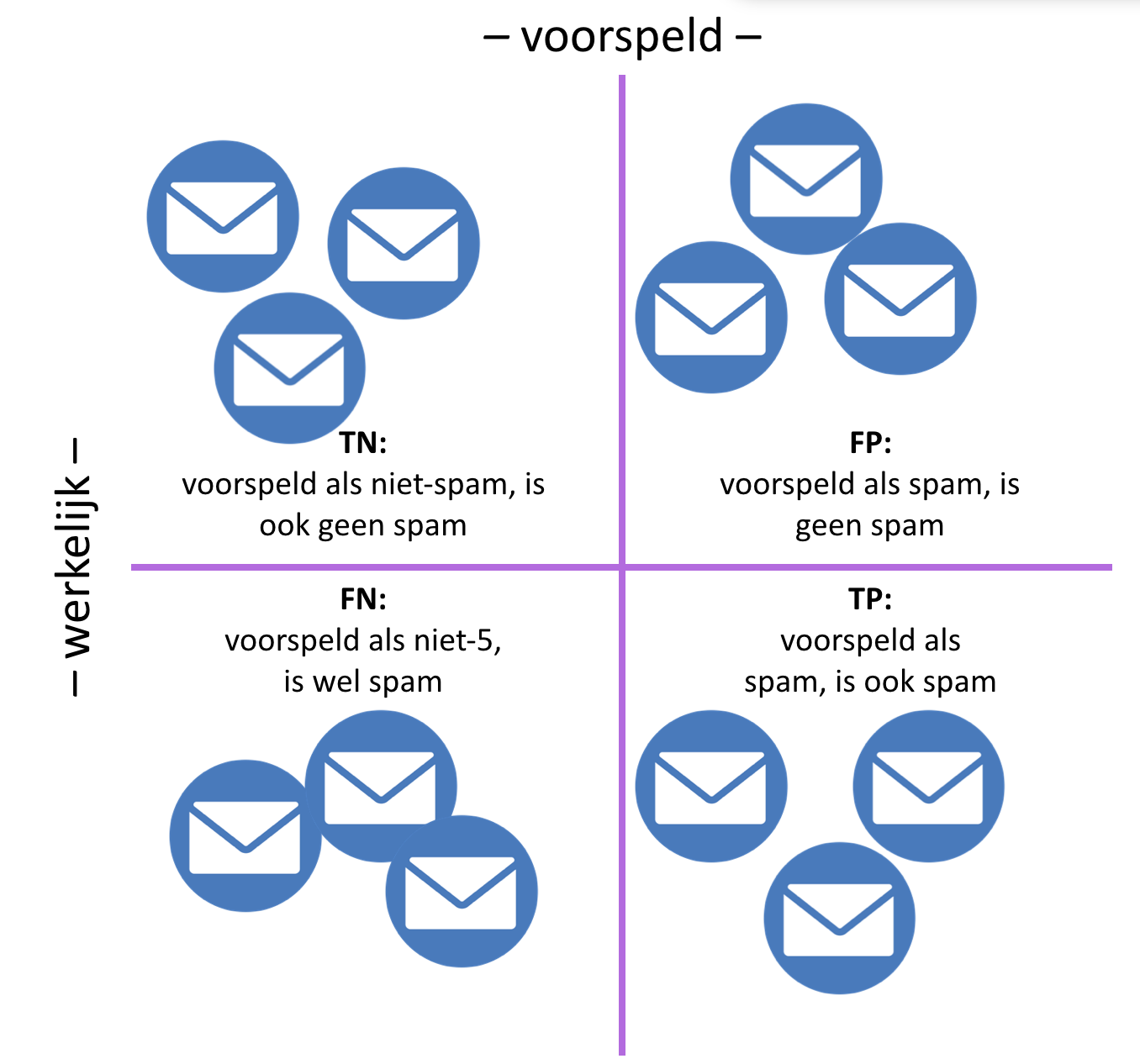
Zoals bekend is de accuratesse op zich niet voldoende om de presentatie van een classifier te bepalen: wanneer je gewoon zou gokken heb je bij tien mogelijke categorieën al een score van tien procent, en als je zou gokken dat een sample iets niet is, is de accuratesse al negentig procent. Betere metrieken hiervoor worden gegeven door de confusion matrix, die tijdens de theorieles besproken is.
Maak eerst de methode load_model() af; deze methode moet het getrainde model laden dat je als laatste stap in de vorige opgave hebt opgeslagen.
Opgave 1a: bepalen van de confusion matrix#
Maak de methode conf_matrix() af. Zoals je ziet krijgt deze methode twee parameters mee, namelijk de door het netwerk voorspelde waarden, en de daadwerkelijke waarden. Maak gebruik van de methode confusion_matrix in TensorFlow om deze matrix te bepalen. Retourneer de matrix.
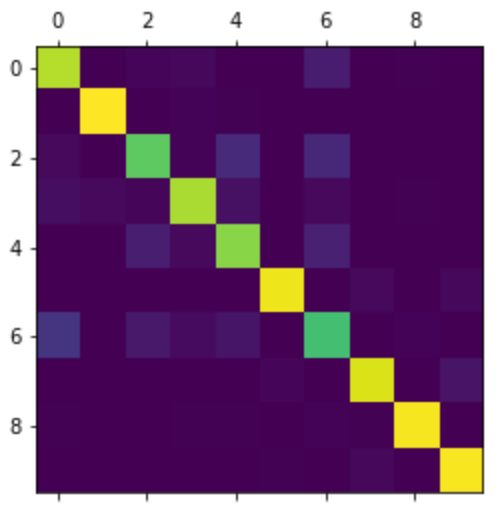
Als je hiermee klaar bent, wordt de methode door het script exercise3.py aangeroepen, met de voorspellingen van de test_images en actuele waarden van die test-data (test_labels). Het resultaat wordt vervolgens in een plot weergegeven; als het goed is, ziet het er ongeveer als volgt uit:
Opgave 1b: TP, TN, FP, FN#
Om meer metrieken uit het getrainde model te halen, volstaat niet alleen het percentage van de samples dat correct is geclassificeerd; we moeten dan ook weten welk percentage terecht als niet van een bepaalde klasse is geclassificeerd, welke onterecht als wel van een bepaalde klasse, en welk percentage onterecht als wel van een bepaalde klasse: de zogenaamde true positives, true negatives, false positives en false negatives (zoals in het theoriecollege besproken is).
De methode conf_els() in uitwerkingen.py krijgt als parameter een numpy-array mee, die ook ten grondslag ligt aan de afbeelding hierboven. De regels van deze matrix corresponderen met de werkelijke waarde van het sample, de kolommen van deze matrix corresponderen met de voorspelling van het sample door het model. Hoewel er semantisch wel het één en ander op aan te merken is, definiëren we de hierboven beschreven metrieken als volgt:
\(tp_{i} = c_{ii}\)
\(fp_{i} = \sum_{l=1}^n c_{li} - tp_{i}\)
\(fn_{i} = \sum_{l=1}^n c_{il} - tp_{i}\)
\(tn_{i} = \sum_{l=1}^n \sum_{k=1}^n c_{lk} -tp_{i} - fp_{i} - fn_{i}\)
Hierbij is \(i\) de categorie in kwestie (dus in dit specifieke geval loopt die van 1 - 10).
Implementeer de methode conf_els(), en retourneer een lijst met deze vier metrieken voor elk label – bestudeer het reeds gegeven deel van de implementatie om een beeld te krijgen van de exacte vorm van de return-waarde.
Opgave 1c: precision en recall#
Implementeer nu de methode conf_data(), waarin je de data die je in de vorige opgave hebt gemaakt omzet in de onderstaande metrieken:
\(precision (PPV) = \frac{tp}{tp + fp}\)
\(recall (sensitivity, TPR) = \frac{tp}{tp + fn}\)
\(specificity (TNR) = \frac{tn}{tn + fp}\)
\(fall-out (FPR) = \frac{fp}{fp + tn}\)
Deze methode krijgt de lijst uit de vorige opgave mee: de totale \(tp\) is dan de som van alle \(tp\)’s van alle labels – en vergelijkbare berekeningen voor de total \(tn\), \(fp\) en \(fn\). Retourneer deze data als een dictionary. Als je deze beide methoden hebt geïmplementeerd, kun je het script exercise3.py nogmaals runnen; Hierdoor worden deze waarden afgedrukt. Zeg op basis van deze resultaten iets over de kwaliteit van het uitgeprogrammeerde netwerk.